Sistem Bilangan Real
Pada bagian ini, pembaca diingatkan kembali pada konsep tentang himpunan. Himpunan adalah sekumpulan obyek/unsur dengan kriteria/syarat tertentu. Unsur-unsur dalam himpunan S disebut anggota (elemen) S. Himpunan yang tidak memiliki anggota disebut himpunan kosong, ditulis dengan notasi { }.
Jika a merupakan anggota himpunan S, maka dibaca “a elemen S”. Jika a bukan anggota himpunan S, maka dibaca “a bukan elemen S”.
Pada umumnya, sebarang himpunan dapat dinyatakan dengan 2 cara. Pertama, dengan mendaftar seluruh anggotanya. Sebagai contoh, himpunan A yang terdiri atas unsur-unsur 1,2,3,4,5,6,7,8,9 dapat dinyatakan sebagai:
Cara yang kedua, yaitu dengan menuliskan syarat keanggotaan yang dimiliki oleh seluruh anggota suatu himpunan tetapi tidak dimiliki oleh unsur-unsur yang bukan anggota himpunan tersebut. Apabila himpunan A di atas dinyatakan dengan cara ini, maka dapat ditulis:
Selanjutnya, akan disampaikan beberapa himpunan bilangan yang dipandang cukup penting.
Sedangkan bilangan phi merupakan hasil bagi keliling sebarang lingkaran terhadap diameternya (Gambar 1.1.2).
Sumber :
http://matematikauniversitas.blogspot.co.id/2013/03/sistem-bilangan-real.html
https://www.google.com/search?q=matematika&source=lnms&tbm=isch&sa=X&ved=0ahUKEwiG-s_Eq6LRAhVMRo8KHToXBOwQ_AUICCgB&biw=1366&bih=634
http://matematikauniversitas.blogspot.co.id/2013/03/sistem-bilangan-real.html
https://www.google.com/search?q=matematika&source=lnms&tbm=isch&sa=X&ved=0ahUKEwiG-s_Eq6LRAhVMRo8KHToXBOwQ_AUICCgB&biw=1366&bih=634
https://www.google.com/search?q=matematika&ie=utf-8&oe=utf-8
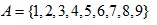

















Mantaabb,, ACC untuk tanggal 1 Des 16,, jangan lupa rapikan tulisannya yaa,, trimkasih
BalasHapusrefrensinya jangan ngambil di satu sumber yaa
BalasHapus