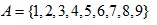MACAM-MACAM MATRIKS adalah judul dari postingan ini. Tegur sapa matematika universitas untuk sahabat sharematika semua. Berjumpa lagi dengan matematika universitas blog yang membahas semua materi matematika universitas atau materi matematika perguruan tinggi. Sebelum kita membahas Macam-macam matriks alangkah baiknya kita berdoa terlebih dahulu.
Matriks adalah salah satu materi dari mata kuliah aljabar linier dan kali ini kita akan membahas salah satu materi dari aljabar linier ini yang berjudul macam-majam matriks.Sebelum kita mempelajari apa saja macam-macam matriks alangkah baiknya kita mengetahui terlebih dahulu apa itu matriks.
Definisi Matriks.
Matriks adalah susunan elemen-elemen yang berbentuk persegi panjang atau persegi yang diatur menurut baris-baris dan kolom-kolom serta ditempatkan dalam tanda kurung biasa atau kurung siku.
Setelah kalian tahu definisi matriks mari kita melangkah ke macam-macam matriks :
Pertama.
Matriks persegi atau Matriks bujur sangkar
Matriks persegi adalah matriks yang memiliki baris dan lajur yang sama bentuknya.
m=n.
Contoh matriks persegi :
Kedua.
Matriks Diagonal.
Matriks diagonal adalah matriks yang unsur-unsurnya semua bernilai nol kecuali pada diagonal utamanya.
Contoh Matriks diagonal:
Ketiga.
Matriks Segitiga.
Matriks segitiga adalah matriks yang semua unsur diatas diagonal utamanya bernilai no, ataupun dibawah diagonal utamanya bernilai nol.
Contoh matriks segitiga :
Keempat.
Matriks Setangkup atau matriks simetris
Matriks satangkup adalah matriks persegi yang unsurnya pada baris ke-i dan ke-j sama nilainya dengan unsur pada kolom ke-j dan ke-i.
Contoh matriks setangkup.
Kelima.
Matriks identitas.
Matriks identitas adalah matriks skalar uang nilai unsur-unsur diagonal utamanya sama dengan satu.
Contoh matriks identitas.
Keenam.
Matriks nol.
Matriks nol adalah matriks yang semua unsur-unsurnya bernilai sama dengan nol.
Contoh matriks nol.
Ketujuh.
Matriks Baris.
Matriks baris adalah matriks yang unsur-unsurnya membentuk suatu baris bilangan.
contoh matriks baris.
( 1 3 2 7 5 )
Kedelapan.
Matriks Kolom.
Matriks kolom adalah matriks yang unsur-unsurnya membentuk suatu kolom.
Contoh matriks kolom.
Setelah kalian tahu definisi matriks mari kita melangkah ke macam-macam matriks :
Pertama.
Matriks persegi atau Matriks bujur sangkar
Matriks persegi adalah matriks yang memiliki baris dan lajur yang sama bentuknya.
m=n.
Contoh matriks persegi :
Kedua.
Matriks Diagonal.
Matriks diagonal adalah matriks yang unsur-unsurnya semua bernilai nol kecuali pada diagonal utamanya.
Contoh Matriks diagonal:
Ketiga.
Matriks Segitiga.
Matriks segitiga adalah matriks yang semua unsur diatas diagonal utamanya bernilai no, ataupun dibawah diagonal utamanya bernilai nol.
Contoh matriks segitiga :
Keempat.
Matriks Setangkup atau matriks simetris
Matriks satangkup adalah matriks persegi yang unsurnya pada baris ke-i dan ke-j sama nilainya dengan unsur pada kolom ke-j dan ke-i.
Contoh matriks setangkup.
Kelima.
Matriks identitas.
Matriks identitas adalah matriks skalar uang nilai unsur-unsur diagonal utamanya sama dengan satu.
Contoh matriks identitas.
Keenam.
Matriks nol.
Matriks nol adalah matriks yang semua unsur-unsurnya bernilai sama dengan nol.
Contoh matriks nol.
Ketujuh.
Matriks Baris.
Matriks baris adalah matriks yang unsur-unsurnya membentuk suatu baris bilangan.
contoh matriks baris.
( 1 3 2 7 5 )
Kedelapan.
Matriks Kolom.
Matriks kolom adalah matriks yang unsur-unsurnya membentuk suatu kolom.
Contoh matriks kolom.